7. Projection, Screen 변환 행렬

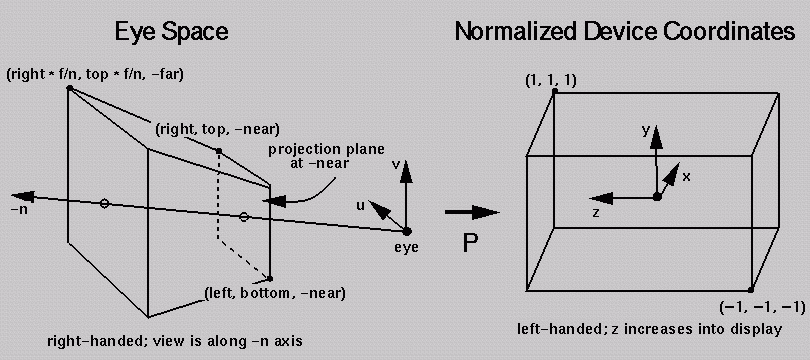
Projection 변환 행렬

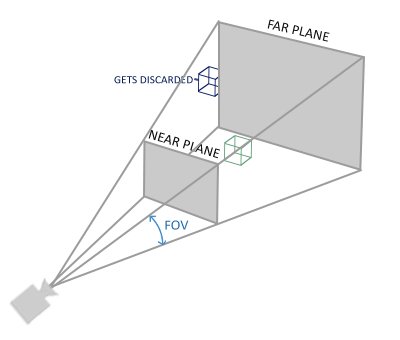
3D 박스에 그려지는 요소들을 2D화면에 비율에 맞춰 그리는 변환이 필요하다.

• Z 기준의 깊이값
• XY 기준 화면의 비율
• XY 기준 화각에 따라 비율
• Z 기준의 near - far사이의 비율

다음 네 가지가 변환 행렬 요소에 들어가야 한다.

깊이값

0 ~ 1 사이의 깊이를 변환

\[X = \frac{x}{z}\] \[Y = \frac{y}{z}\]

화면 비율

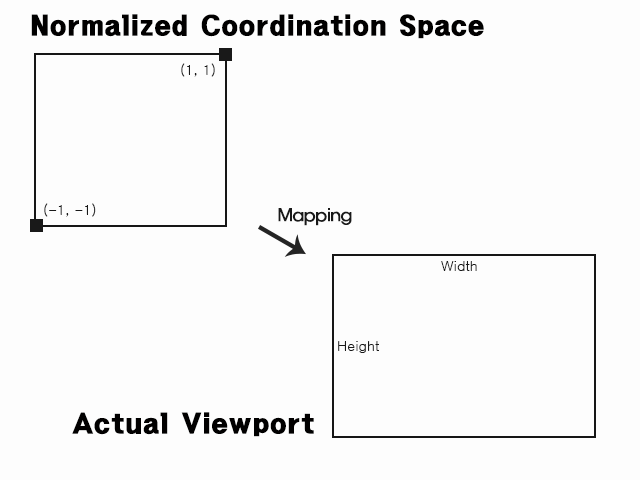
-1 ~ 1의 화면 비율을 뷰포트로 보여주는 800x600으로 변환

\[r = \frac{w}{h}\] \[X = \frac{x}{r\cdot z}\] \[Y = \frac{y}{z}\]

Y에는 r를 곱하지 않아도 된다. 한 쪽을 기준으로 다른 한쪽은 고정된 쪽으로 비율에 맞춰 변환시키기 때문이다.

FOV(화각)에 따른 비율

\[tan(\frac{\theta}{2})\] \[X = \frac{x}{r\cdot z \cdot tan(\frac{\theta}{2})}\] \[Y = \frac{y}{z\cdot tan(\frac{\theta}{2})}\]

선형 공식을 성립하려면 $X=ax+b$가 성립되어야 한다.
하지만 위 식에서는 z값이 들어가면서 선형공식이 성립되지 않고 있다.
따라서 z의 값은 따로 빼고 행렬을 먼저 구성해보자.

\[(x, y, z, w)\times \begin{pmatrix} \frac{x}{r\cdot tan(\frac{\theta}{2})}& 0 & 0 & 0\\ 0 & \frac{x}{r\cdot tan(\frac{\theta}{2})} & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix}\]

z값을 살리기 위해 $m_{33}$ 에 1넣는다.
\(= (\frac{x}{r\cdot tan(\frac{\theta}{2})\cdot z}, \frac{x}{r\cdot tan(\frac{\theta}{2})\cdot z}, \frac{z}{z}, 1)\)

하지만 이럴 경우 유효한 z값이 사라진다.
따라서 z값을 유지시킬 방법을 우회적으로 찾아야 한다. 그것이 w값이다.

\[(x, y, z, w)\times \begin{pmatrix} \frac{x}{r\cdot tan(\frac{\theta}{2})}& 0 & 0 & 0\\ 0 & \frac{x}{r\cdot tan(\frac{\theta}{2})} & 0 & 0\\ 0 & 0 & 1 & 1\\ 0 & 0 & 0 & 0\\ \end{pmatrix}\]

z값을 살리기 위해 $m_{34}$ 에 1넣는다.

near - far비율

\[(x, y, z, w)\times \begin{pmatrix} \frac{x}{r\cdot tan(\frac{\theta}{2})}& 0 & 0 & 0\\ 0 & \frac{x}{r\cdot tan(\frac{\theta}{2})} & 0 & 0\\ 0 & 0 & A & 1\\ 0 & 0 & B & 0\\ \end{pmatrix}\]

A와 B를 넣고 near-far를 뽑아보자!.

\[= (\frac{x}{r\cdot tan(\frac{\theta}{2})}, \frac{x}{r\cdot tan(\frac{\theta}{2})}, Az+B, z)\]

전체 요소 z를 나눠준다.

\[= (\frac{x}{r\cdot tan(\frac{\theta}{2})\cdot z}, \frac{x}{r\cdot tan(\frac{\theta}{2})\cdot z}, A+\frac{B}{z}, 1)\]

다음 식이 성립한다.

\[G(z) = A +\frac{B}{z}\]

near와 far는 각각 0, 1이다.

\[A(near) = 0\] \[B(far) = 1\] \[A(near) = A +\frac{B}{n} = 0\] \[B(far) = A +\frac{B}{f} = 1\]

$A(near) = A +\frac{B}{n} = 0$를 통해 $A = -\frac{B}{n}$, $B = An$이라는 것을 유추 할 수 있다.

이 값을 far값이 대입해보자.

\[A +\frac{-An}{f} = 1\] \[A(\frac{f-n}{f}) = 1\] \[A = \frac{f}{f-n}\]

\[-\frac{B}{n} +\frac{B}{f} = 1\] \[B(\frac{-f+n}{nf}) = 1\] \[B = \frac{-nf}{f-n}\]

최종적인 Projection 변환 행렬의 모습니다.

\[(x, y, z, w)\times \begin{pmatrix} \frac{x}{r\cdot tan(\frac{\theta}{2})}& 0 & 0 & 0\\ 0 & \frac{x}{r\cdot tan(\frac{\theta}{2})} & 0 & 0\\ 0 & 0 & \frac{f}{f-n} & 1\\ 0 & 0 & \frac{-nf}{f-n} & 0\\ \end{pmatrix}\]

다음 네 가지에 대한 정보가 담겨 있다.

1. Z값 깊이 값
2. 화면 비율
3. FOV 화각에 따른 비율
4. Near-Far 비율

WVP(World-Camera-Projection)를 행렬 연산 한번에 연산해둔 뒤, Local에 있는 오브젝트를 해당 연산을 통해 한 번에 Screen까지 가져올 수 있다. 인제 이것을 화면에 보여지는 ScreenSpace로 옮겨보자.

Screen 변환 행렬

Projection->Viewport

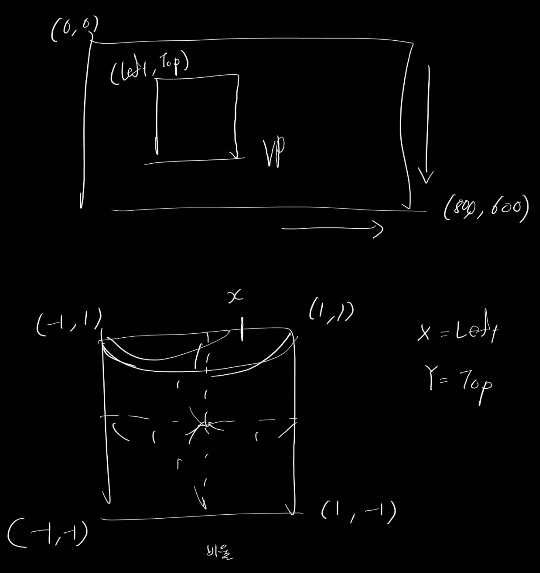
\[X = Left + \frac{x+1}{2}W\] \[Y = Top + \frac{y-1}{2}W\]

y-1을 하는 이유?
그래픽스 좌표계와 화면 좌표계의 차이가 있다.
NDC에서는 Y값이 위가 + 아래가 -
화면 좌표계는 Y값이 위가 0 아래가 증가.
화면좌표계로 넘어가고 있기 때문에 뒤집어야 한다.

Z값의 Min-Max값이 필요하다.

\[Z=Min+Z(Max-Min)\]

Z의 Min, Max값을 어디 사용할까? 두 개의 뷰포트를 활용하여 범위를 임의로 정해서 그리지 않도록 할 수도 있음. 거의 사용하는 경우는 없다고 한다.

다음을 행렬로 표현하면

\[X = Left + \frac{xw}{2}+\frac{w}{2}\] \[Y = Top + \frac{yW}{2}-\frac{W}{2}\]

결론

\[(x, y, z, w)\times \begin{pmatrix} \frac{w}{2}& 0 & 0 & 0\\ 0 & \frac{w}{2} & 0 & 0\\ 0 & 0 & Max-Min & 1\\ Left+\frac{w}{2} & Top-\frac{w}{2} & Min & 0\\ \end{pmatrix}\]