6. World, View 변환 행렬

변환 과정

Local -> World -> Camera -> Projection -> clip -> viewport

• Local : 오브젝트 자기 자신을 기준으로 한 세상
• World : 게임 세상
• Camera : 카메라가 바라보는 특정 영역에서의 세상
• Projection(원교 투영, 직교 투영) : -1~1의 비율에 맞춰진 세상
• Viewport(해상도) : 800x600의 화면에 보여지는 세상

Local To World

기저벡터를 할용한 좌표계 변환 행렬을 이용한 방식

RVW라고 사용한 것을 의미있는 명명으로 수정하였다.
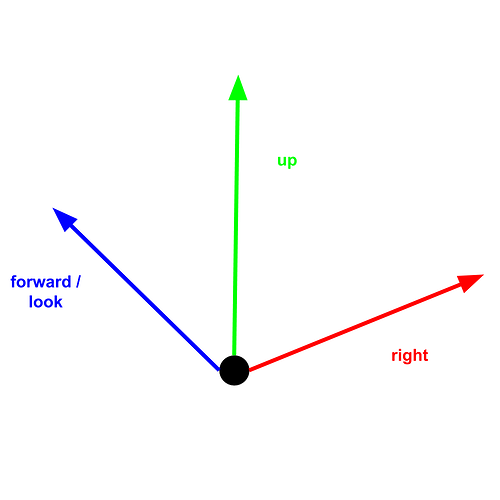
RightVector, UpVector, LookVector로 표현을 각각 R, U, L로 표현하자.

\[(x, y, z, w)\times \begin{pmatrix} R_{x}& R_{y} & R_{z} & 0\\ U_{x} & U_{y} & U_{z} & 0\\ L_{x} & L_{y} & L_{z} & 0\\ Q_{x} & Q_{y} & Q_{z} & 1\\ \end{pmatrix}\]

$Q_x$, $Q_y$, $Q_z$ 는 B좌표계 기준 A의 좌표

$R U V$ 는 B좌표계 기준 A의 단위 벡터를 의미한다.

이것을 기저 벡터라고 부르기도 한다.

Scale값이 필요하다면, 추가로 Scale행렬을 곱해야 한다.

SRT 변환 행렬을 이용한 방식.

World 행렬만 봐도, Posision, Rotation, Scale을 알 수 있고 반대로, Position, Rotation, Scale로 World행렬을 구할 수 있다.
SRT행렬을 곱해도 World변환이 가능하다.

아래 내용부터는 Scale은 1이라고 가정하고, 연산 표현을 쓰지 않는다. RT연산에 대한 내용이다.

World To Camera

기저벡터를 할용한 좌표계 변환 행렬을 이용한 방식

카메라를 왼쪽으로 이동하며 카메라에 비친 오브젝트는 오른쪽으로 이동하는 것처럼 보인다.

카메라를 y축 기준 시계 방향으로 회전하면 오브젝트는 카메라 기준 반시계 방향으로 공전하는 것처럼 보인다.

즉, 카메라를 이동하는 것 = 월드 전체를 반대로 이동시키는 것

그러면 모든 오브젝트에 역행렬을 곱해야 한다는 것을 의미한다.

\[(RT)^- = T^- \cdot R^-\]

RT의 역행렬을 의미한다.

SRT 변환 행렬을 이용한 방식.

카메라는 월드 중심 좌표에 가만히 있고, 오브젝트가 움직인다고 가정해보자.

카메라의 로컬 좌표계 안에 오브젝트들이 움직인다고 볼 수 있다.
즉, 카메라의 월드 행렬의 역행렬을 이용해 오브젝트를 CameraSpace에 넣을 수 있다.

결론

카메라 회전 행렬은 직교행렬이다.
XYZ가 90도로 수직인 행렬을 의미한다.
직교행렬의 역행렬은 전치행렬이라는 특징을 가지고 있다.
따라서 $T^- \cdot R의 전치행렬$를 의미한다.

\[Camera변환행렬 = Camera의 World^- = RT^- = T^- \cdot R^-\]

T의 역행렬은 Q요소를 반대로 뒤집기만 하면 된다.

\[\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ -Q_{x} -& Q_{y} & -Q_{z} & 1\\ \end{pmatrix}\]

R의 역행렬(R의 전치행렬)은 아래와 같다.

\[\begin{pmatrix} R_{x}& U_{y} & L_{z} & 0\\ R_{y} & U_{y} & L_{z} & 0\\ R_{z} & U_{z} & L_{z} & 0\\ 0 & 0 & 0 & 1\\ \end{pmatrix}\]

벡터의 연산으로 표현하면 둘의 내적으로 표현할 수 있다.
최종적인 Camera변환 행렬은 아래와 같다.

\[T^-\times R^- = \begin{pmatrix} R_{x}& U_{y} & L_{z} &0\\ R_{y} & U_{y} & L_{z} & 0\\ R_{z} & U_{z} & L_{z} & 0\\ \overrightarrow{-C}\cdot \overrightarrow{Right} & \overrightarrow{-C}\cdot \overrightarrow{Up} & \overrightarrow{-C}\cdot \overrightarrow{Look} & 1\\ \end{pmatrix}\]

또 다른 방법(XMMatrixLookAtLH함수 활용하기).

XMMatrixLookAtLH 함수

XMMATRIX XM_CALLCONV XMMatrixLookAtLH(
  [in] FXMVECTOR EyePosition,
  [in] FXMVECTOR FocusPosition,
  [in] FXMVECTOR UpDirection
) noexcept;

[in] EyePosition : 카메라의 위치입니다.

[in] FocusPosition : 초점의 위치입니다.

[in] UpDirection : 카메라의 위쪽 방향(일반적으로 < 0.0f, 1.0f, 0.0f >)

카메라 위치, 카메라가 바라보는 초점의 위치, 카메라의 위쪽 방향을 이용하여 카메라 뷰 space변환 행렬을 구할 수 있다.

카메라의 위치와 초점의 위치를 통해 LookVector를 구한 뒤,

LookVector와 UpDirection의 외적을 통해 RightVector를 구한다.

UpDirection은 LookVector와 RightVector의 수직인 벡터가 아님으로 외적을 위해 UpVector를 구한다.