5. 좌표계 변환
인프런 Rookiss C++과 언리얼로 만드는 MMORPG 게임 개발 시리즈 게임 수학과 DirectX12을 듣고 리뷰한 내용입니다.
좌표계 변환 행렬
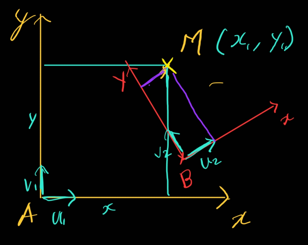
최종적으로 그려지는 단계까지 좌표계를 변환하는 과정을 거쳐야 한다. 따라서 좌표계 변환을 어떻게 하는지 연습해볼 필요가 있다.
$\overrightarrow{U_{1}}$ ,$\overrightarrow{V_{1}}$ 을 B를 기준으로 한 벡터로 변환해서 생각해보자.
$\overrightarrow{U_{1}}$가 가진 $(x, y)$의 값을 $\overrightarrow{U_{2}}$로 치환
$\overrightarrow{V_{1}}$가 가진 $(x, y)$의 값을 $\overrightarrow{V_{2}}$로 치환
$\overrightarrow{AM} = \overrightarrow{AB} + \overrightarrow{BM}$을 다시 대입해보면,
\[\overrightarrow{AM}= x_{1}\cdot(U_{x}\cdot\overrightarrow{U_{2}} + U_{y}\cdot\overrightarrow{V_{2}}) + y_{1}\cdot(V_{x}\cdot\overrightarrow{U_{2}} + V_{y}\cdot\overrightarrow{V_{2}})\]다음 식을 풀면,
\[\overrightarrow{AM}= x_{1}\cdot U_{x}\cdot\overrightarrow{U_{2}} + x_{1}\cdot U_{y}\cdot\overrightarrow{V_{2}} + y_{1}\cdot V_{x}\cdot\overrightarrow{U_{2}} + y_{1}\cdot V_{y}\cdot\overrightarrow{V_{2}}\]다음 식을 $\overrightarrow{U_{2}}$ $\overrightarrow{V_{2}}$ 로 묶어서 표현하면,
\[\overrightarrow{AM}=(x_{1}\cdot U_{x}+y_{1}\cdot V_{x})\overrightarrow{U_{2}} + (x_{1}\cdot U_{y}+y_{1}\cdot V_{y})\overrightarrow{V_{2}}\]$\overrightarrow{AM} = \overrightarrow{AB} + \overrightarrow{BM}$이므로,
\[\overrightarrow{AB}+\overrightarrow{BM} = (x_{1}\cdot U_{x}+y_{1}\cdot V_{x})\overrightarrow{U_{2}} + (x_{1}\cdot U_{y}+y_{1}\cdot V_{y})\overrightarrow{V_{2}}\]$-\overrightarrow{AB}=\overrightarrow{BA}$ 를 만족하므로,
\[\overrightarrow{BM} = (x_{1}\cdot U_{x}+y_{1}\cdot V_{x})\overrightarrow{U_{2}} + (x_{1}\cdot U_{y}+y_{1}\cdot V_{y})\overrightarrow{V_{2}} + \overrightarrow{BA}\]$\overrightarrow{BA}$은 B를 기준으로 한 A방향의 선분이라고 볼 수 있음으로 $\overrightarrow{U_{1}},$ $\overrightarrow{V_{1}}$ 를 $\overrightarrow{U_{2}},$$\overrightarrow{V_{2}}$로 변경 가능하다.
\[\overrightarrow{BA} = Q_{x}\cdot\overrightarrow{U_{2}} + Q_{y}\cdot\overrightarrow{V_{2}}\] \[\overrightarrow{BM} = (x_{1}\cdot U_{x}+y_{1}\cdot V_{x})\overrightarrow{U_{2}} + (x_{1}\cdot U_{y}+y_{1}\cdot V_{y})\overrightarrow{V_{2}} + (Q_{x}\cdot\overrightarrow{U_{2}} + Q_{y}\cdot\overrightarrow{V_{2}})\]다음 식을 정리하면
\[\overrightarrow{BM} = (x_{1}\cdot U_{x}+y_{1}\cdot V_{x}+Q_{x})\overrightarrow{U_{2}} + (x_{1}\cdot U_{y}+y_{1}\cdot V_{y}+Q_{x})\overrightarrow{V_{2}}\]$\overrightarrow{BM} = x_{2} \cdot \overrightarrow{U_{2}} + y_{2}\cdot\overrightarrow{V_{2}}$을 만족하고 있음으로
\[x_{2} \cdot \overrightarrow{U_{2}} + y_{2}\cdot\overrightarrow{V_{2}} = (x_{1}\cdot U_{x}+y_{1}\cdot V_{x}+Q_{x})\overrightarrow{U_{2}} + (x_{1}\cdot U_{y}+y_{1}\cdot V_{y}+Q_{x})\overrightarrow{V_{2}}\]즉, 다음 식이 성립한다.
\[x_{2} = (x_{1}\cdot U_{x}+y_{1}\cdot V_{x}+Q_{x})\] \[y_{2} = (x_{1}\cdot U_{y}+y_{1}\cdot V_{y}+Q_{x})\]이것을 행렬 공식으로 써보면 다음과 같다. (위 계산과정은 2차원을 고려하였음, 아래 행렬은 z요소를 추가하여 썼다.)
\[(x, y, z, w)\times \begin{pmatrix} U_{x}& U_{y} & U_{z} & 0\\ V_{x} & V_{y} & V_{z} & 0\\ W_{x} & W_{y} & W_{z} & 0\\ Q_{x} & Q_{y} & Q_{z} & 1\\ \end{pmatrix}\]다음 행렬 공식을 토대로 좌표계가 변환된다.
위치 변환의 경우 $(x, y, z, 1)$을 곱한다.
방향 변환의 경우 $(x, y, z, 0)$을 곱한다.
마지막 요소에 0을 곱하면 $Q_{x}$, $Q_{y}$, $Q_{z}$요소에 어떤 값이 있더라도 0으로 모두 초기화되는 형태를 보이게 된다.
따라서 방향에 대한 좌표계 변환이 이루어지게 된다.
$Q_{x}$, $Q_{y}$, $Q_{z}$요소의 정보로 $\overrightarrow{BA}$에 대한 정보를 알 수 있음.
$U_{x}$, $U_{y}$, $U_{z}$ -> $\overrightarrow{U}$의 좌표
$V_{x}$, $V_{y}$, $V_{z}$ -> $\overrightarrow{V}$의 좌표
$W_{x}$, $W_{y}$, $W_{z}$ -> $\overrightarrow{W}$의 좌표에 대한 정보를 알 수 있음.