3. 행렬

행렬에 대한 이해

3D 세상이 있는 물체를 카메라의 각도에 따라 2D화면으로까지의 변환 과정 벡터의 변화 과정을 행렬로 묘사할 수 있다는 것을 의미한다. 또한 여러 행렬을 겹쳐서 표현이 가능하다.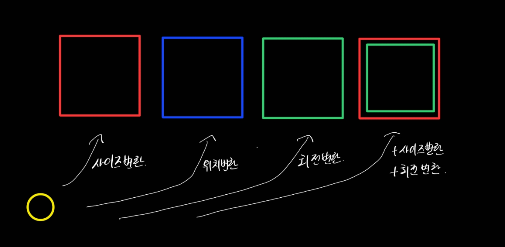

행렬 정의

2차원 배열 스칼라 값이 들어가 있음. 행수와 열수를 정해줘야 함.
행(Row), 열(Col) 2x3

행렬과 스칼라 곱

\[M = \begin{pmatrix} 1 & 3 \\ 4 & 2 \\ \end{pmatrix} \times K = \begin{pmatrix} K & 3K \\ 4K & 2K \\ \end{pmatrix}\]

행렬과 행렬 덧셈

\[A = \begin{pmatrix} 1 & 3 \\ 4 & 2 \\ \end{pmatrix} B = \begin{pmatrix} 1 & 1 \\ 1 & 1 \\ \end{pmatrix}\]

\[A+B = \begin{pmatrix} 1 + 1 = 2 & 3 + 1 = 4 \\ 4 + 1 = 5 & 2 + 1 = 3 \\ \end{pmatrix}\]

위 두 가지는 게임 수학에서 거의 다루진 않음. 행렬X행렬이 가장 중요하다!!!!

행렬 x 행렬

\[{A}_{m\times n} \times B_{n\times p} = C_{m\times p}\]

\[{A}_{m\times n} = \begin{pmatrix} a_{1,1}& \cdots & a_{1,n} \\ \vdots & & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix}{B}_{n\times p} = \begin{pmatrix} b_{1,1}& \cdots & b_{1,p} \\ \vdots & & \vdots \\ b_{n,1} & \cdots & b_{n,p} \end{pmatrix}\]

\[\begin{pmatrix} a_{1,1}& \cdots & a_{1,n} \\ \vdots & & \vdots \\ a_{m,1} & \cdots & a_{m,n} \end{pmatrix} \ \times \begin{pmatrix} b_{1,1}& \cdots & b_{1,p} \\ \vdots & & \vdots \\ b_{n,1} & \cdots & b_{n,p} \end{pmatrix} = \begin{pmatrix} c_{1,1}& \cdots & c_{1,p} \\ \vdots & & \vdots \\ c_{m,1} & \cdots & c_{m,p} \end{pmatrix}\]

A행렬과 B행렬 간의 곱을 할 때 A는 왼쪽에서 오른쪽, B는 위에서 아래로 값을 서로 쌍으로 차례로 값을 곱하고 더한 값이다.

\[c_{1,1} = a_{1,1} \times b_{1,1} \cdots a_{1,n}\times b_{n,1}\]

다음 식을 아래 식으로 표현 가능.

\[C_{ij} = \sum_{k=1}^{n} a_{ik}b_{kj}\]

시그마 : k가 1부터 n까지 k가 1 씩 덧셈 한다는 것을 표현. 1 + 2 + 3. .. k \(\sum_{k=1}^{n}k\)

행렬의 곱의 표현을 내적으로 표현 가능 R : row, C : column \(\overrightarrow{R}3 \times \overrightarrow{C}3\)

연습

\({A_{2\times2}} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix}\)

\({B_{2\times1}} = \begin{pmatrix} 1 \\ 2 \\ \end{pmatrix}\)

\(AB = \begin{pmatrix} 1 + 4 \\ 3 + 8 \\ \end{pmatrix}= \begin{pmatrix} 5 \\ 11 \\ \end{pmatrix}\)

교환법칙, 결합법칙

행렬의 곱은 교환법칙이 성립하지 않는다. 2X2행렬과 2X1행렬의 곱은 가능하다.
하지만 2X1행렬과 2X2행렬은 곱셈이 성립되지 않는다.

다만, 결합 법칙 (AB)C = A(BC)

대각 행렬(diagonal matrix)

\[\begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{pmatrix}\]

단위 행렬(identity matrix) ; I

\[\begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}\] \[A\times I = A\] \[A\times I = I\times A\]

곱셈에서 1을 곱하면 자기 자신이 나오는 것처럼 단위행렬을 곱하면 자기자신 행렬이 나온다.

4X4행렬! - 정사각형 행렬

4X4행렬을 사용하는 이유는 무엇일까?

\(\overrightarrow{V}(x, y, z, 1)\)
벡터는 보통 위와 같은 형태가 되어있다. 1X4행렬의 형태이다.

1X4행렬에 4X4행렬을 곱하여 벡터를 변환한 결과값은 1X4행렬의 형태로 나온다.

즉, 변환 과정으로 나온 결과값이 이전 행렬의 포멧과 이후 행렬의 포멧은 같고, 행렬의 값는 변환된다.

단위행렬의 중요성

AB = I MAB = M(AB) = MI = M

M X M^-1 = I MA에 B를 곱하면 M으로 원래 값으로 돌아감. B은 역행렬이라고 할 수 있다.

역행렬이 가능하지 않을 수도 있다.
역행렬이 가능한 행렬을 가역행렬이라고 하고, 역행렬이 불가능한 행렬을 불가역행렬이라고 한다.

뒤로 되돌리고 싶을 때 사용하는게 역행렬이라고 생각하자!!

역행렬의 특징

\[MM^{-1} = I = M^{-1}M\]

일반적으로 행렬의 교환법칙은 성립하지 않는다.
하지만 위와 같은 경우는 가능하다. 아래는 증명

\[MM^{-1}M = IM = M\] \[MI = M\]

역행렬을 구하는 공식! determinant

\[A = \begin{pmatrix} a & b \\ c & d \\ \end{pmatrix}\]

역행렬 가능 조건 \(Det = ad - bc \neq 0\)

\[A^{-1} = \frac{1}{D}\begin{pmatrix} d & -b \\ -c & a \\ \end{pmatrix}\]

연습

\[{A} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix}\]

\[D = 4 - 6 = -2 \neq 0\]

\[{A^{-1}} = \frac{1}{-2} \begin{pmatrix} 4 & -2 \\ -3 & 1 \\ \end{pmatrix} = \begin{pmatrix} 2 & 1 \\ \frac{3}{2} & -\frac{1}{2} \\ \end{pmatrix}\]

\[{A} = \begin{pmatrix} 1 & 2 \\ 3 & 4 \\ \end{pmatrix} \times \begin{pmatrix} 2 & 1 \\ \frac{3}{2} & -\frac{1}{2} \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 \\ 0 & 1 \\ \end{pmatrix}\]

2X2행렬은 간단하지만 4X4행렬은 더 복잡하다.

전치행렬(Transpose)

행렬 대각을 기준으로 뒤집은 형태

\[\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \\ \end{pmatrix} \implies \begin{pmatrix} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \\ \end{pmatrix}\]

특징 1. \((M^{T})^{T} = M\)

특징 2. \((MN)^{T} = N^{T}M^{T}\)

직교행렬

\[M\begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{pmatrix}\]

(0 0 1) $\overrightarrow{V_{1}}$
(1 0 0) $\overrightarrow{V_{2}}$
(0 1 0) $\overrightarrow{V_{3}}$

$\overrightarrow{V_{1}}\cdot\overrightarrow{V_{2}} = 0$
$\overrightarrow{V_{2}}\cdot\overrightarrow{V_{3}} = 0$
$\overrightarrow{V_{1}}\cdot\overrightarrow{V_{3}} = 0$

내적이 0 이면 90도이다. 즉 직교형태라는 것을 의미한다.

$M\cdot M^{T} = M^{T}\cdot M = I$

\[M\begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ \end{pmatrix} \times M^{T}\begin{pmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ \end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{pmatrix}\]

직교상황인 경우 전치행렬을 곱하면 단위행렬이 나온다. $M\cdot M^{T} = I$

즉, 전치행렬은 역행렬이라는 것을 의미하기도 한다. $M^{T} = M^{-1}$