2. 벡터

Vector

Vector란

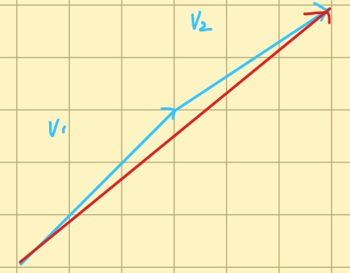
크기와 방향

\[\overrightarrow{V} = \overrightarrow{AB}\]

벡터 표시를 위해 위에 화살표로 표시한다.

\[\overrightarrow{V} = \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} Bx - Ax \\ By - Ay \end{pmatrix}\]

목적지 좌표에서 시작지 좌표를 뺴면 Vector를 구할 수 있다.

Vector 계산

벡터끼리 덧셈과 뺄셈은 가능하지만, 곱셈과 나눗셈은 불가능하다.

\[\overrightarrow{A} + \overrightarrow{B} = \overrightarrow{B} + \overrightarrow{A}\] \[\overrightarrow{A} - \overrightarrow{B} = \overrightarrow{B} - \overrightarrow{A}\]

벡터의 교환,결합 법칙이 성립
\(3 \times \overrightarrow{B}\)

다만, 벡터와 스칼라끼리는 곱셈과 나눗셈이 가능하다.

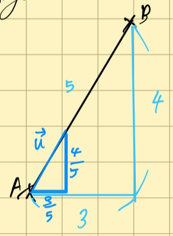
단위 벡터

normalize

플레이어의 속도(스칼라) x 방향 벡터를 통해 사용함

\[\overrightarrow{V} = \begin{pmatrix} 3 \\ 4 \end{pmatrix}\]

\[단위 벡터 - \begin{pmatrix} \frac{3}{5} \frac{4}{5} \end{pmatrix}\]

내적과 외적

내적

dot
결과값 : 스칼라

각도랑 연관성이 높다. 빛에 닿았을 떄, 그림자의 각도를 잴 때 사용함.

벡터 사이의 점은 곱샘이 아닌 내적의 표현
| | 은 벡터의 크기를 나타내는 표현

\[\overrightarrow{A}\cdot\overrightarrow{B}\] \[= |\overrightarrow{A}|\cdot|\overrightarrow{B}|\cdot\cos \theta\] \[= A_{x}B_{x} + A_{y}B_{y}\] \[= A\cdot B\cdot\cos \theta\]

B가 단위 벡터로 1이라고 했을 때,

$A\cdot 1\cdot\cos \theta$ 의 값을 손쉽게 추출할 수 있다.

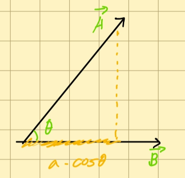
사잇각을 알아내려고 할 때,

양수인지 음수인지에 따라 90도를 넘는지 아닌지 판단

내적의 값이 0일 때,

90도 270도라는 것을 의미.

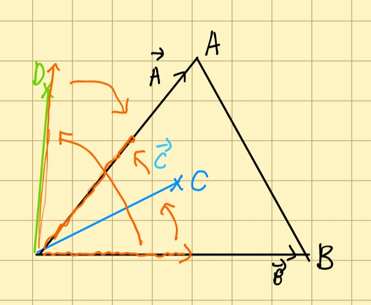
외적

법선 벡터 - 두 벡터의 수직인 벡터, 교환법칙이 성립하지 않음, 방향이 뒤바뀜 \(\overrightarrow{A}\times\overrightarrow{B}\)

\[= |\overrightarrow{A}|\cdot|\overrightarrow{B}|\cdot\sin \theta\] \[\overrightarrow{A}\times\overrightarrow{B} \neq \overrightarrow{B}\times\overrightarrow{A}\]

영역 안에 있는지 확인할 때

\[반시계방향 :\overrightarrow{B}\times\overrightarrow{C} / 반시계방향 : \overrightarrow{C}\times\overrightarrow{A}\] \[반시계방향 :\overrightarrow{B}\times\overrightarrow{D} / 시계방향 : \overrightarrow{D}\times\overrightarrow{A}\]

위치

Vec3 {float x, float y, float z} 형태.
기하 벡터, 위치 벡터 두 가지를 표현함.

기하 벡터 : 크기와 방향
위치 벡터 : 위치 표시 position