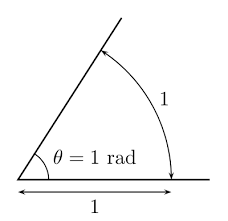1. 삼각함수

삼각함수

1. 피타고라스 정리

$h^2 = a^2 + o^2$

플레이어와 몬스터 간의 거리를 구한다. 기본적으로 피타고라스 정리.

---

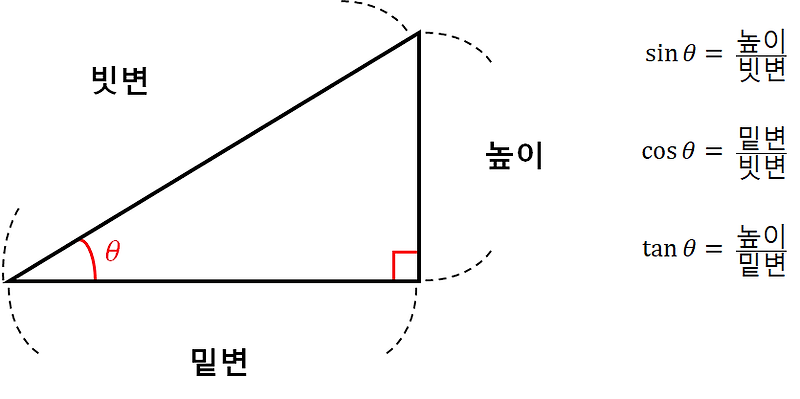
2. $\cos\theta$, $\sin\theta$, $\tan\theta$ 삼각비

삼각비 기준각을 기준으로 두 변의 길이 비율을 구하는 것

빗변, 높이, 밑변의 비율.

\[\cos\theta = \frac{밑변}{빗변}\] \[\sin\theta = \frac{높이}{빗변}\] \[\tan\theta = \frac{높이}{밑변} = \frac{\sin\theta}{\cos\theta}\]

---

3. 원 그리기

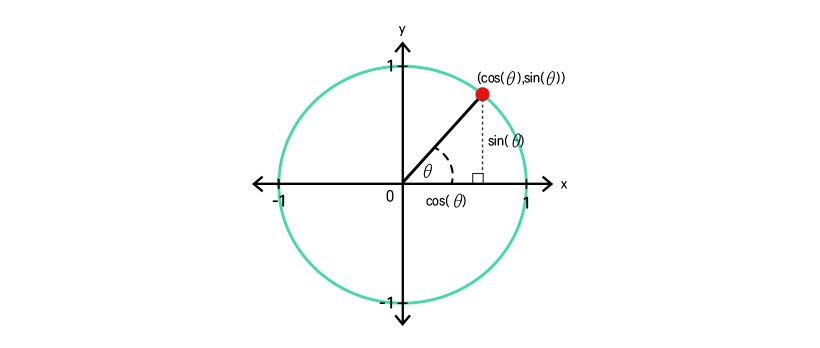
$0^\circ ~ 360^\circ$ => 라디안으로 표현.

라디안

\[360^\circ = 2\pi\] \[\pi \approx 3.14\] \[1 rad \approx 57\] \[2\pi = 360^\circ\] \[\pi = 180^\circ\] \[\frac{\pi}{3} = 60^\circ\] \[\frac{\pi}{4} = 45^\circ\] \[\frac{\pi}{6} = 30^\circ\]

코사인의 특징.

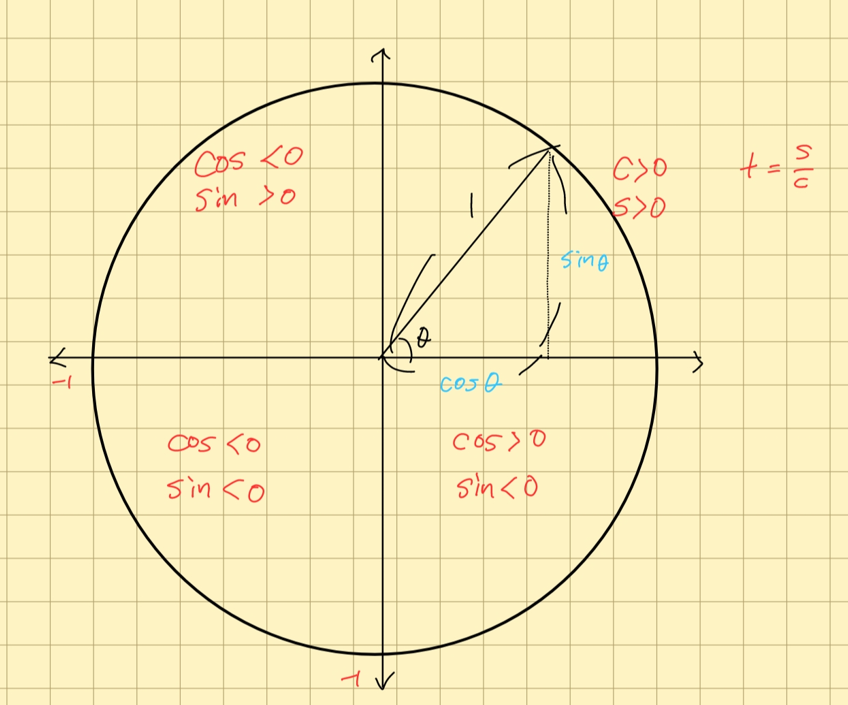
$\cos(\theta) = \cos(-\theta)$ -> 짝함수, 우함수 $f(x) = f(-x)$

$\sin(\theta) = -\sin(-\theta)$ -> 홀함수, 기함수 $f(x) = -f(-x)$

---

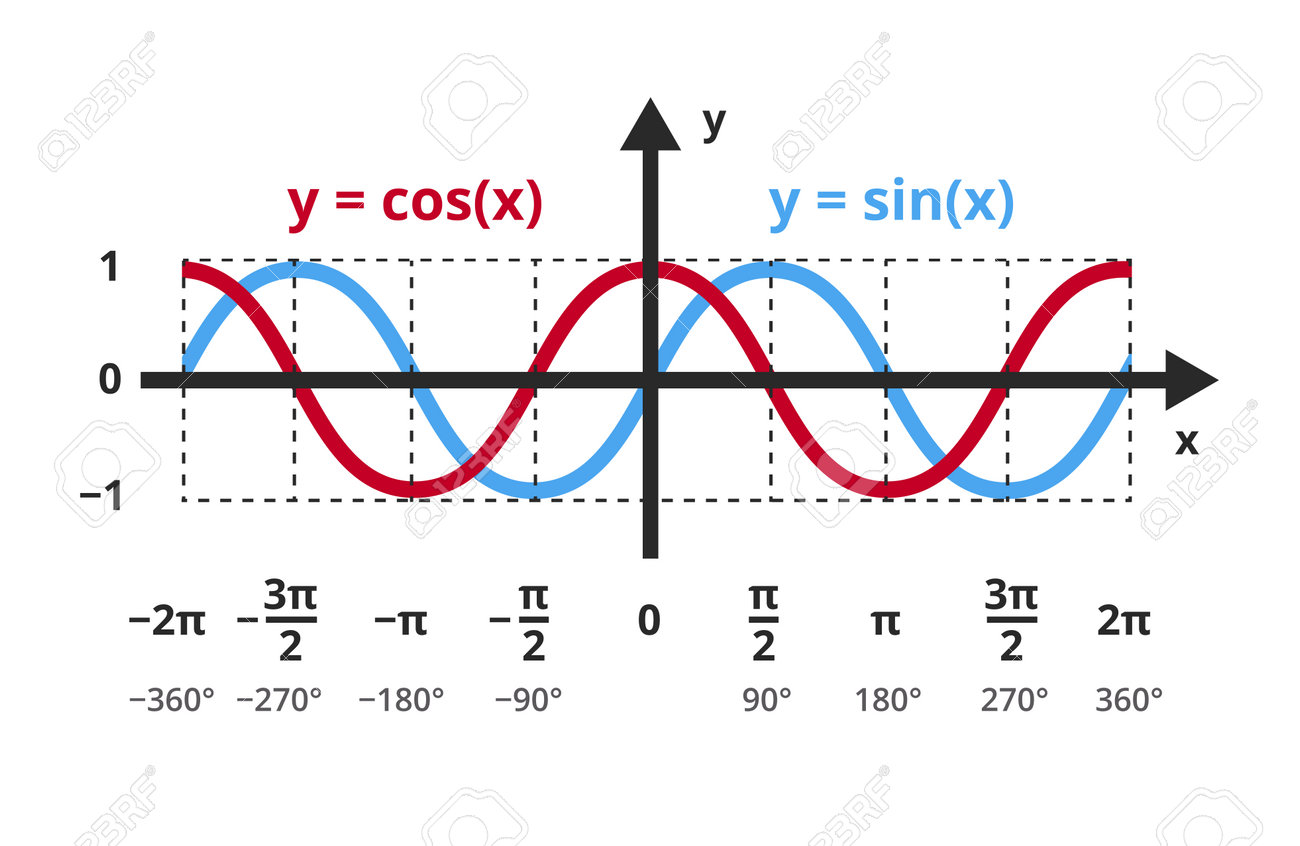
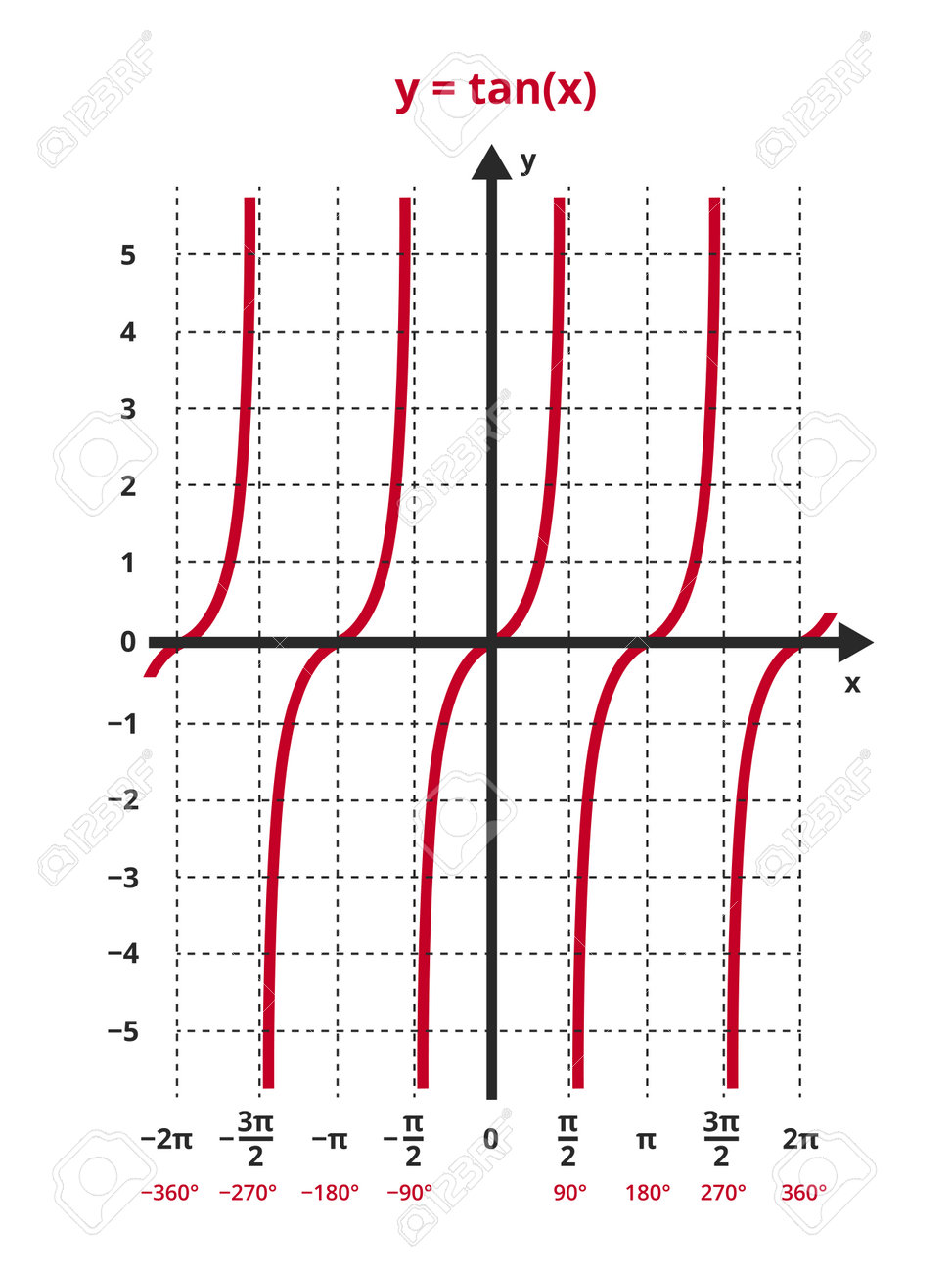
3. 삼각함수 그래프

각도 별 cos, sin의 값을 나타낸 그래프.

그래프가 좌우로 무한이 이어짐 특정 각도에서 2pi 만큼 회전을 하더라도 그대로 위치로 옴. 2pi를 주기로 파동이 일어남.

sin 그래프 왼쪽으로 이동 : $\sin\left( \theta + \frac{\pi}{2} \right) = \cos\theta$ 그래프

sin 그래프 오른쪽으로 이동 : $\sin\left( \theta-\frac{\pi}{2} \right) = -\cos\theta$

그래프의 이동으로 sin과 cos그래프가 겹치는 경우가 발생한다.

---

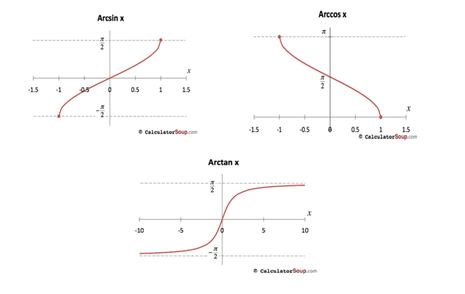
4. 삼각함수 역함수

$\infty < \theta < \infty$ -> -1 ~ 1

비율을 알고 어떤 각도인지 알려고 할 때

$\cos\theta = ?$

$\sin\theta = ?$

$? \to \theta$

$\arccos(?) = \theta$
-> 0 ~ 2$\pi$

$\arcsin(?) = \theta$

-> $-\frac{\pi}{2}$ ~ $\frac{\pi}{2}$

$\arctan(?) = \theta$

-> $-\frac{\pi}{2}$ ~ $\frac{\pi}{2}$

각도 -> 비율 : cos, sin, tan 비율 -> 각도 : arccos, arcsin, arctan

범위가 중요함. 하나를 넣으면 하나의 값이 나와야 한다. 하지만 여러 값이 가능함. 예를 들어 arccos일 때, 2pi, 4pi…

---

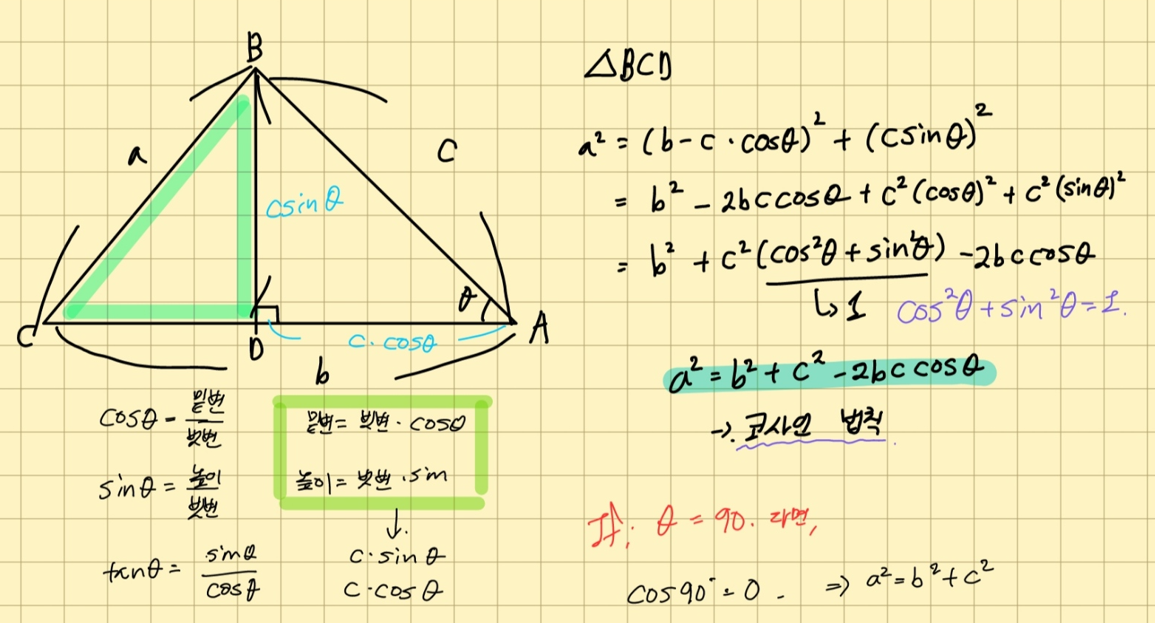
5. 코사인 법칙

피타고라스 정리의 일반화

---

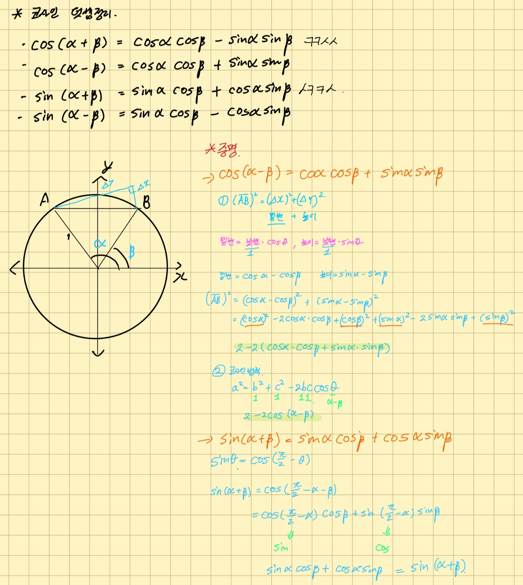
6. 코사인 덧셈정리

\(\cos(\alpha + \beta) = \cos\alpha \cos\beta - \sin\alpha \sin\beta\)
\(\cos(\alpha - \beta) = \cos\alpha \cos\beta + \sin\alpha \sin\beta\)
\(\sin(\alpha + \beta) = \sin\alpha \cos\beta + \cos\alpha \sin\beta\)
\(\sin(\alpha - \beta) = \sin\alpha \cos\beta - \cos\alpha \sin\beta\)